Een tijdje terug heb ik mijn idee om een maand lang de reistijden bij te houden op het traject Rotterdam Lombardijen – Leiden Centraal met jullie gedeeld. Dat onderzoek duurde heel oktober lang, en inmiddels is het 31 oktober en kan ik de uitslagen dus met jullie delen. Als jullie willen weten hoe ik het heb aangepakt, verwijs ik jullie terug naar die blog. Deze gaat met name over de resultaten en een flink stuk statistiek. Maar maak je niet druk – ik loods jullie erdoorheen!
Allereerst begin ik met de gemiddelden met jullie te delen. Ik neem aan dat jullie wel weten wat een gemiddelde is, en anders raad ik jullie aan eens beter op te letten bij rekenen/wiskunde. Ik heb twee dingen bijgehouden: de verwachte reis en de eigenlijke reis. De verwachte reis is zoals hij werd aangegeven op de reisplanner, de eigenlijke reis is wat mijn stopwatch me liet weten, naar minuten afgerond. Het gemiddelde van de verwachte reistijd is 50,93 minuten. Het gemiddelde van de eigenlijke reistijd is 53,50 minuten.
Maar, wat betekent dit precies? Is dit een groot verschil, is dit een klein verschil, is het gemiddeld? Laten we eerlijk wezen – eigenlijk kunnen we dat niet precies zeggen. Gelukkig hoeft dat ook niet.
Wetenschappers hebben een toets ontwikkeld waarmee je twee gemiddelden tegen elkaar af kan zetten. Deze toets heet de t-toets. Hoe dat precies in zijn werk gaat, dat gaat per ingewikkelde formules die ik niet uit mijn hoofd ken en ik wil het niet te complex maken. We houden het dus even op de t-toets.
Eén voorwaarde van de t-toets is dat beide variabelen normaal verdeeld moeten zijn. Met andere woorden: als ik een t-toets op dit onderzoekje wil uitvoeren, dan moeten zowel de verwachte als de eigenlijke reistijd normaal verdeeld zijn. Wat is normaal verdeeld precies? Symmetrisch verdeeld. Bij een ideale normaal verdeelde variabele ligt er evenveel rechts van het gemiddelde als links. In een boxplot – een bepaalde grafiek – ziet een ideale normaal verdeelde variabele er zo uit: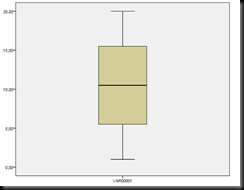
Let op hoe perfect symmetrisch het is. Die streep in de rechthoek, die de rechthoek tot twee vierkantjes maakt, ligt op de plaats van het gemiddelde. De streep helemaal onderaan, waar de lijn ophoudt, is het minimum, en de streep bovenaan is het maximum.
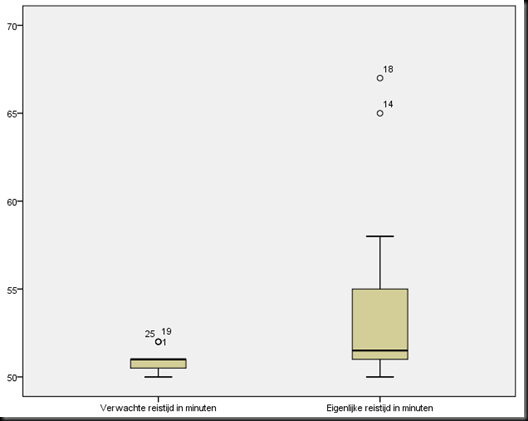
Dus, nu terug naar het onderzoekje. De eerste vraag – zijn de verwachte reistijd en de eigenlijke reistijd normaal verdeeld? Nou… kijk maar naar de boxplot hieronder…
De linkerboxplot – die halve boxplot – is van de verwachte reistijd. Het ziet er niet uit als een normale boxplot, maar dat komt omdat het programma een beetje vervelend doet – je mag er op basis hiervan prima van uitgaan dat de verwachte reistijd symmetrisch is.
De rechterboxplot, de eigenlijke reistijd, is zeer zeker niet symmetrisch. Er zit veel meer boven de middelste streep dan eronder. Daarbuiten zie je nog twee rondjes helemaal bovenaan: dat zijn uitbijters, getallen die zo ver van het gemiddelde af liggen dat het programma ze niet helemaal meerekent. (Dat is ook foutgegaan bij de linkerboxplot)
Dus, niet symmetrisch en daarmee niet normaal verdeeld. Is nu alles verloren? Nee, niet echt. De t-toets is over het algemeen redelijk robuust. Met andere woorden, het kan best tegen een ietwat scheve verdeling. Toch hou ik rekening met deze absoluut niet-normale verdeling, want het kan de resultaten wel beïnvloeden. Daarom doe ik er nog een tweede test bij: de Wilcoxon-test. Deze test is een stuk minder betrouwbaar, maar een normale verdeling is niet nodig. Omdat de t-test betrouwbaarder is hou ik die er wel bij.
Goed, die twee toetsen dus. Nogmaals, hoe die precies in hun werk gaan, daar ga ik verder niet op in. Wat wel belangrijk is om te weten om de tabellen straks af te kunnen lezen, is dat beide toetsen werken met kansen. Want, het verschil in gemiddelden hier kan door toeval komen. Hoe groot mag de kans dat het toeval is maximaal zijn? Wetenschappers – en ik ook – gaan meestal uit van een kans van 5%. Is de kans dat het toeval is groter dan 5%, dan is het onderzoek ongeldig. Met andere woorden, is de kans groter dan 5%, dan moet ik op basis van dat resultaat concluderen dat de vertraging niet zoveel uitmaakt.
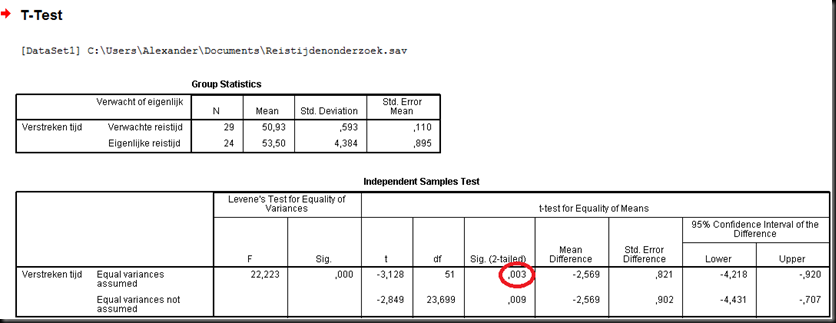
Klaar? Hier komen de beide tabellen. Deze is van de T-toets:
(Ik heb de bovenste tabel alleen bijgevoegd voor de mensen die ècht geïnteresseerd zijn in de statistiek en er alles van weten. De leken hier hoeven alleen te letten op het getal in het rode cirkeltje)
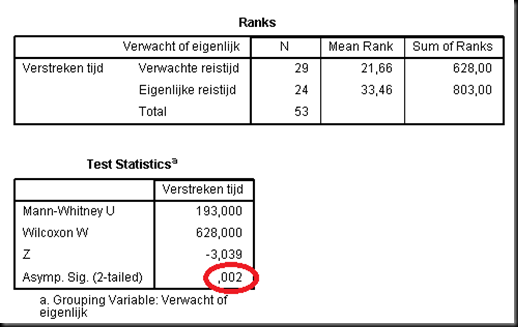
En van de Wilcoxon-test:
(Zelfde verhaal – bovenste tabel is niet belangrijk, let alleen op het getal in het rode cirkeltje)
Welke conclusie kunnen we uit deze data dus trekken? De toetsen zijn het op dit punt helemaal met elkaar eens – de kans dat dit verschil toeval is en niet belangrijk is kleiner dan vijf procent. Dus ja, er is een significant verschil. Was het niet significant geweest, dan waren die getallen in de rode cirkeltjes ,05 of hoger geweest. Maar dat is niet het geval.
Dus ja, als ik de volgende keer klaag over de NS op het traject Lombardijen-Leiden, dan is dat gegrond. Het verschil doet ertoe en de NS moet er iets aan doen, op basis van deze data.
Maar wacht, ik had nog een ding getest. Was er WiFi of niet, en deed die het of niet? Het antwoord is: in 61% van de treinreizen was er WiFi. In 76% van de gevallen deed de WiFi het ook. Is dat veel? Is dat weinig? Dat laat ik aan jullie interpretatie over, want daar zijn geen toetsen voor. Maar, wat ik er zelf over te zeggen heb is dat de WiFi er veel vaker was dan ik had verwacht, en ook dan ik me kan herinneren van vorig jaar. Had ik de toets vorig jaar gedaan, dan was het getal véél lager uitgevallen. En 76% van de gevallen vind ik persoonlijk niet heel erg weinig. 1 op de 4 keer doet de WiFi niet, nou, dat is geen ramp als de andere 3 keren de WiFi naar behoren werkt. 100% was natuurlijk ideaal geweest, maar hé, WiFi is apparatuur en dat wil best wel eens stuk gaan.
Dus, ik mag niet meer klagen over de WiFi, maar ik mag naar hartelust mopperen als de trein weer eens te laat komt, volgens deze test. Het verschil is significant en niet op toeval berust. Er moet dus echt iets aan gedaan worden, ook vanuit een wetenschappelijk oogpunt.
Kan ik nog meer doen? Zeker. Ik zou kunnen kijken of er meer vertraging op de heenreis was dan op de terugreis. Ik zou kunnen kijken of de verwachte reistijd bij de terugreis korter is. Maar punt is, daar heb ik geen behoefte aan. Mijn onderzoek ging erover of er een significant verschil is in de echte reistijd vergeleken met de verwachte reistijd, en die is er. Maar ik kan begrijpen dat andere mensen nu nieuwsgierig zijn naar de data. Om daar zelf mee te toetsen, of gewoon nieuwsgierigheid in het algemeen. Daarom voeg ik een tabel bij met alle data. Even verduidelijking: een aantal keren ben ik vergeten mijn stopwatch te starten of te stoppen, en één keer ben ik vergeten de WiFi te controleren. De keren dat ik mijn stopwatch vergat staan aangegeven als 999 – het programma waar ik mee werk telt die 999’s niet mee. Het niet WiFi-gecontroleerd-geval staat gewoon aangegeven als 9, en dat betekent ook hier weer dat het niet door het programma is meegerekend.
Verder betekent 3 bij de WiFi dat er geen WiFi was, 2 dat die WiFi er wel was maar het niet deed, en 1 dat er WiFi was die naar behoren werkte. De meest rechtse kolom, tenslotte, staat voor de heen- of de terugreis: 1 is heenreis, 2 is terugreis. Er mist één terugreis, omdat ik daar eerder uit moest stappen omdat ik nog iets daar te doen had. Die telde ik dus bewust niet mee.
Goed, hier komt dus de tabel:
| Dag | Verwachte reis | Eigenlijke reis | WiFi | Heen of terug |
| 1 | 52 | 52 | 1 | 1 |
| 1 | 50 | 50 | 1 | 2 |
| 2 | 50 | 52 | 1 | 1 |
| 2 | 50 | 52 | 3 | 2 |
| 3 | 50 | 51 | 3 | 1 |
| 3 | 51 | 58 | 3 | 2 |
| 4 | 51 | 999 | 1 | 1 |
| 4 | 51 | 51 | 2 | 2 |
| 5 | 51 | 51 | 1 | 1 |
| 5 | 51 | 53 | 1 | 2 |
| 6 | 52 | 999 | 2 | 1 |
| 6 | 51 | 51 | 2 | 2 |
| 7 | 51 | 51 | 2 | 1 |
| 7 | 50 | 65 | 2 | 2 |
| 8 | 51 | 999 | 9 | 1 |
| 8 | 51 | 51 | 3 | 2 |
| 9 | 51 | 54 | 1 | 1 |
| 9 | 51 | 67 | 1 | 2 |
| 10 | 52 | 55 | 1 | 1 |
| 10 | 51 | 56 | 1 | 2 |
| 11 | 51 | 50 | 3 | 1 |
| 11 | 51 | 51 | 1 | 2 |
| 12 | 51 | 51 | 3 | 1 |
| 12 | 51 | 999 | 1 | 2 |
| 13 | 52 | 55 | 3 | 1 |
| 14 | 51 | 999 | 3 | 1 |
| 14 | 51 | 55 | 3 | 2 |
| 15 | 51 | 51 | 3 | 1 |
| 15 | 50 | 51 | 3 | 2 |
Eén kleine aanvulling nog: op de terugreis van 15 oktober(dag 7) en op de heenreizen van 23 en 25 oktober(dagen 11 & 12) was de trein vóór de trein die ik moest hebben zo vertraagd dat ik een trein eerder had. Die vertraging heb ik opgeteld bij de data die ik toen had. Op dag 7 was dat 11 minuten extra, op dag 11 was dat 5 en op dag 12 3 minuten erbij.
Ik hoop dat jullie met mijn blog iets wijzer zijn geweest(wel of niet in de statistiek, maar in ieder geval betreffende het traject Lombardijen-Leiden). En zelf begrijp ik de stof ook een stuk beter nu ik het toe heb kunnen passen, gelukkig. En ik weet nu ook iets meer over de NS – ik ben met andere ogen gaan kijken naar iets waar ik normaal gesproken heel normaal naar kijk. Dus wat dat betreft is mijn doel zeker bereikt.
Genoeg over het reistijdenonderzoek! Morgen is het NOVEMBER en dat betekent dat ik aan de NaNoWriMo mag! Ik ben heel benieuwd hoe het gaat werken, wens me heel veel succes en ik spreek jullie de volgende blog weer!